International Encyclopedia of Systems and Cybernetics

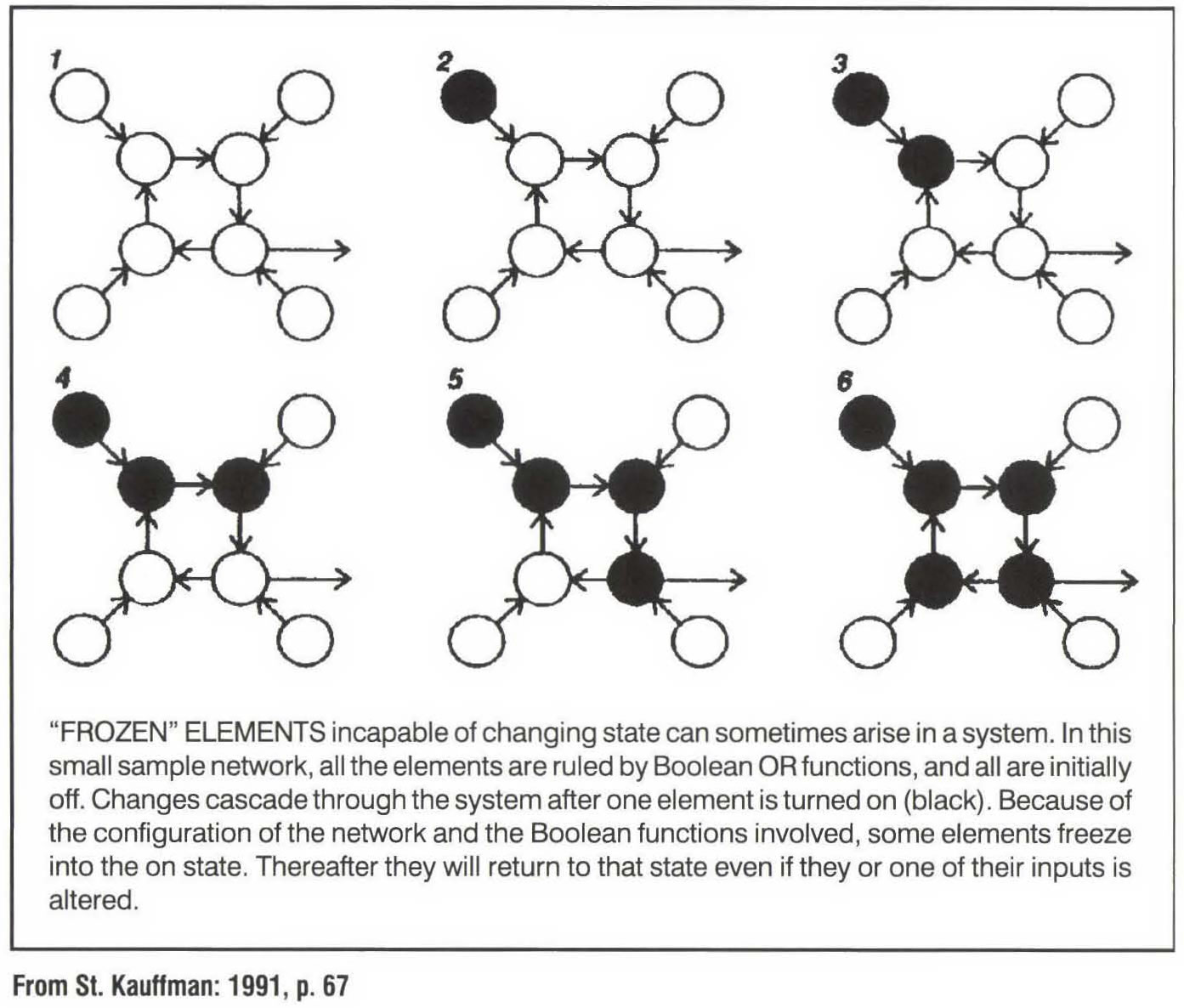
"A connected mesh of elements, each frozen in either the 1 or the 0 state" (St. KAUFFMAN, 1993, p.203).

St. KAUFFMAN describes frozen cores as follows: "The frozen core creates spanning, or percolating walls of constancy which break the system into functionally isolated islands of unfrozen elements cut off from influencing one another by the walls of frozen elements" (1993, p.203).

He adds: "Systems may lie in the ordered regime with frozen components, in the chaotic regime with no frozen components, or in the boundary region between order and chaos where frozen components just melt. The existence of this phase transition suggests that the boundary region might be a particularly interesting region for useful behavior in complex parallel-processing networks… The central idea is that, if a network is deep in the frozen phase, then little computation can occur within it. At best, each small unfrozen, isolated island engages in its own internal dynamics functionally uncoupled from the rest of the system by the frozen component. In the chaotic phase, dynamics is too disordered to be useful… At the boundary between order and chaos, the frozen regime is melting and the functionally isolated unfrozen islands are in tenuous shifting contact with one another. It seems plausible that the most complex, most integrated, and most evolvable behavior might occur in this boundary region" (p.219).

As a resulting hypothesis, KAUFFMAN proposes that "Ecosystems coevolve to the edge of chaos" (p.261).

These views are closely connected with PRIGOGINE's: See hereafter: "Frozen structure".