International Encyclopedia of Systems and Cybernetics

"A topological theory describing the change of a system's structure along a continuous morphogenetic landscape, including occasional jumps" (K. KRIPPENDORFF, 1986, p.9).

In R. THOM's, founder of the theory, words: "It gives a kind of local description of a system within a control parameters space. One may modify the controls on the basis of a certain system of values and describe, through the choice of convenient surfaces in this space, the continuous variations and the occurring catastrophes" (1993, p.30).

THOM thus defines the elementary catastrophe: "Any conflict situation between local regimes, potential minima, which may occur in a stable manner on the four dimensional space-time" (1974, p.71).

K.B.DE GREENE states: "Catastrophe-theoretic models deal with systems that show multiequilibrium behavior and usually show a path irreversibility (hysteresis)" (1990, p.55).

Catastrophe theory is a formalized geometrical theory that cannot even be sketched within the limits of this work (see R. THOM's, E.C. ZEEMAN's and T. POSTON and I. STEWART's references) Let us only try to describe its nature and the wide scope of its applications, as well as to warn against its improper metaphorical uses.

T.F.H. ALLEN and Thomas B. STARR explain it as: "A theoretical construct used for the description of certain types of disjunct behavior. It derives from a topological consideration of folded surfaces describing the interactions between variables. Catastrophe theory is rather specific in its appropriate application, although it serves a more general usefulness as a mathematical metaphor" (1982, p. 263).

F. HEYLIGHEN observes: "It was developed by R. THOM (1975) in order to model the continuous) development of (discontinuous) forms in organisms, thus extending the much older work of the biologist D'ARCY THOMPSON (1917)" (F. HEYLIGHEN, 1997, p.33)

Catastrophe theory is undoubtly a systemic one, since it addresses to a wide field of general phenomena, starting from a qualitative topological view and giving them a common basic ground through isomorphic models. It is basically a theory of discontinuous phenomena, related to sudden phase transitions, marking a jump from one attractor to another. It is closely related with the following topics: Field gradients leading to singularities; markovian systems and LIAPOUNOV stability; bifurcations and unfoldment; morphologies and morphogenesis; and the different corresponding attractors.

The best known part of catastrophe theory are the seven basic elementary catastrophes, upon which according to THOM a general catastrophe theory is to be built upon. (in ZEEMAN, 1977, p,633)

The seven elementary catastrophes (a synthesis of THOM's (1974) and ZEEMAN's (1977) presentations):

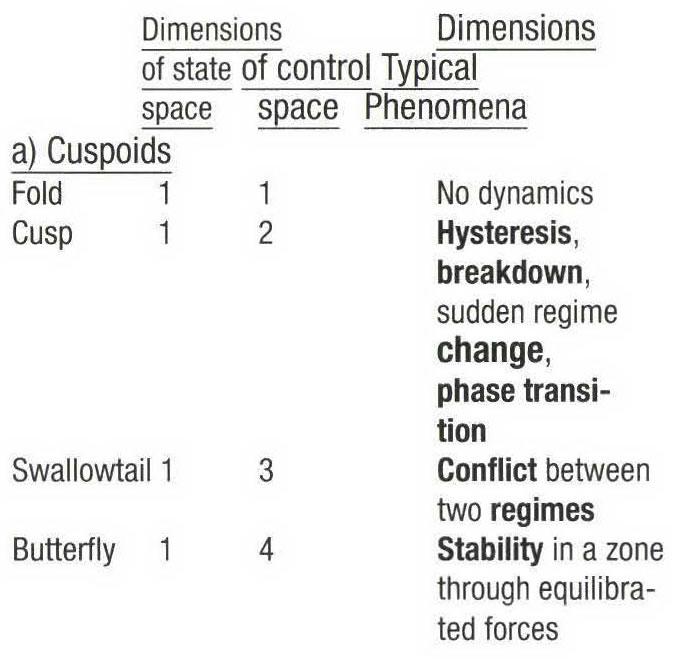
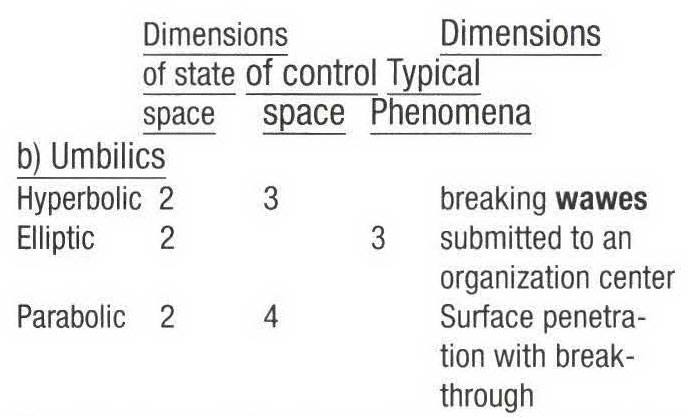
Graphical models have been produced by THOM (1972).

Numerous applications of the elemental catastrophes have been proposed in physics and chemistry (the relation to dissipative structuration and bifurcations in far from equilibrium systems is still a fuzzy area); in engineering; in biology and embryology; in animal and human ethology; in psychology (perception and behavioral shifts) and in social sciences (economics, markets shifts).

However, J. CASTI observes that there have been "… attempts by practitioners to use the theory as a vehicle for predictions in situations where it can at best be used only to explain" (1994, p.48).

In effect, in some cases – undoubtly and at least partly due to the "mediatic" name given by THOM to his theory – the catastrophe models became a somewhat misused and abused metaphor.